TECO东元电机-东元变频器-teco东元电机股份有限公司官网

本文介紹了一種用于顏料/塑料、涂料、油墨計算機配色的軟件SRICI—PPI的基本光學原理及其算法。該軟件以Kubelka-Munk理論的雙常數法為基礎，采用三刺激值相等條件下推導出的矩陣方程計算配方。其準確度經與國外兩種不同類型光學理論為基礎的顏料配色軟件平行比較，具有令人滿意的結果。試驗證明，不同類型的光學理論并非是軟件配色準確度的唯一決定因素，而采用更為復雜的3—flux理論進行設計的軟件并不能從性能/價格比上取得明顯的改進。

一、顏料配色軟件SRICI—PPI的光學理論基礎和算法

顏料的計算機配色不同于染料/紡織品，由于下述兩個原因，使問題大大復雜化：⑴顏料是以粒子形態存在于被著色物質中，因而顏料粒子的散射作用(Scattering)在配色中起著極其重要的作用。

(2)顏料可應用于塑料、涂料、油墨等多種方面，其著色介質多種多樣，有的要求有完全的遮蓋力，有的卻對透明度有一定的要求。因此，可用于染料/紡織品配色的較為簡單的Kubelka-Munk理論的單常數方法就不再適用。

顏料配色軟件SRICI-PPI的光學理論基礎是Kubelka-Munk理論的雙常數法:

二、SRICI-PPI配色軟件準確度評價

SRICI-PPI的配色準確度以下述兩套國外配色軟件作平行對比加以評價：

(1)目前國際市場上出售的顏料系統均以Kubelka-Munk理論的雙常數法為基礎，美國MILTONROY/DIANOMM-350配色系統的顏料配色軟件包即是其中之一，它的配色準確度已在其分布于世界各地的用戶中得到承認。

(2)CIBA-GEIGY公司的物理研究中心和顏料部發展出一套新型的顏料配色軟件CGREC，其光學理論基礎是ChandrsSekhar’s幅射傳輸方程(在層狀介質中)：

三、討論

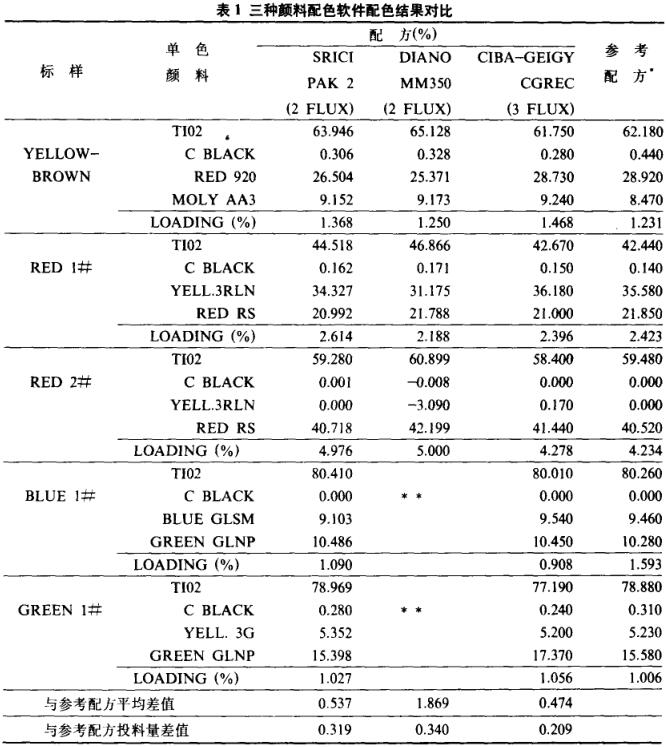
1.對采用以2-fluxKubelka-Munk理論為基礎的配色計算方法是否能滿足工業實際應用的準確度要求，歷來存在不同看法。然而，在配色軟件SRICI-PPI編制過程中，對Kubelka-Munk模式進行適當的修正，這樣算得的配方與基于3-flux模式的軟件CGREC計算的配方并無明顯的差別，這一差異要小于基于相同光學理論模式(2-flux)的軟件SRICI-PPI與MM-350所計算的配方之間的差異(見表1)。事實表明，盡管Kubelka-Mimk理論的假設與實際情況有差異，但在其基礎上發展的配色軟件計算的預測配方的誤差比起工業加工過程中其它因素所造成的誤差還是比較小的，因此在工業界實際應用中被普遍接受。如果采用更為復雜的3-flux或multi-flux理論來配色，復雜性將大大增加，勢必需要功能更為強大的計算機和更為復雜的軟件，這無疑會增加配色系統的硬件、軟件成本，而只能帶來有限的準確度上的改進?因而，時至今日，以2-fluxKubelka-Munk理論為基礎的顏料配色軟件在這一領域的國際市場上和實際應用中仍然占主導地位。

2.將三種配色軟件的配色結果與參考配方相比，從與參考配方平均濃度差值可以看出CIBA-GEIGY的CGREC軟件計算出的配方最接近參考配方，本院開發的SRICI-PF>I次之，美國MILTONROY/DIANOMM-350PAK2的差值稍大。

3.以3-flux理論為基礎的CGREC軟件的最大特點是可以計算出的比較準確的顏料投料量(ColourantLoading),這不僅對配半透明的色樣很重要，在SRICI-PPI軟件中，通過引人參數a，選取正確的絕對散射S，同樣可以得到類似的結果(見表丨中LOADING數據和參考配方投料量差值).

四、結論

以2-fluxKubelka-Munk理論雙常數法為基礎的顏料配色軟件SRICI-PPI經試驗具有令人滿意的配色準確度。以2-flux模式為基礎的配色方法與以3-flux模式為基礎的配色方法之間在配色準確度上的差異并不大于基于同樣2-flux模式的軟件之間的差異，比較起工業加工過程中其它原因所造成的誤差也少得多?因而并不值得采用3flux模式去開發復雜得多的配色軟件和增加硬件開支去爭取有限的改進。